Next time you have a few minutes--waiting for your flight at the airport, or the school bus, or suppertime maybe--use the spare minutes to enjoy some numbers: Find the square root of a fraction, by improving an initial guess. It can be quite entertaining to watch Frrraction at work on a real piece of mathematics as it follows your commands!
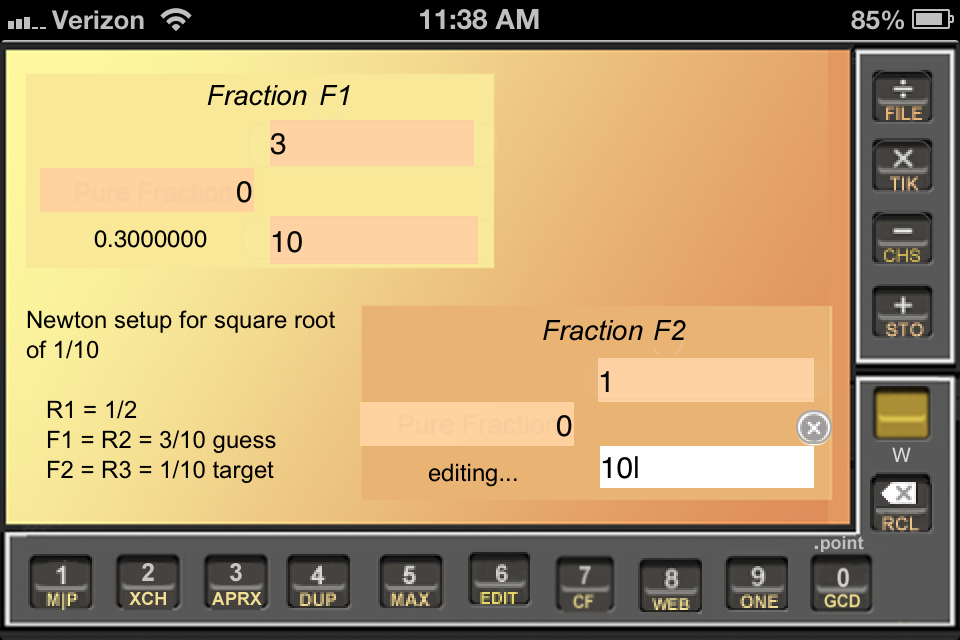
Fig. WYW1 shows the setup for the square root of 0.1, starting with the initial guess 0.3 (whose square is 0.09, fairly close to the target).

Newton (yup, he's the calculus guy who in 1696 became keeper of the King's mint in the Tower of London) proposed a good method, shown in detail in Fig. WYW2. As shown in the on-screen Note, the way we got from Fig. WYW1 to Fig. WYW2 was to divide (F2 by F1) then add (F1 to the result); then we hauled 1/2 out of R1 into F1 and multiplied (by the 19/30 in F2) to get 19/60. The square of 19/60 is 0.1002777--which you can find by doing { Y DUP F2 x }--which is noticeably closer to 0.1 than the original 0.09.
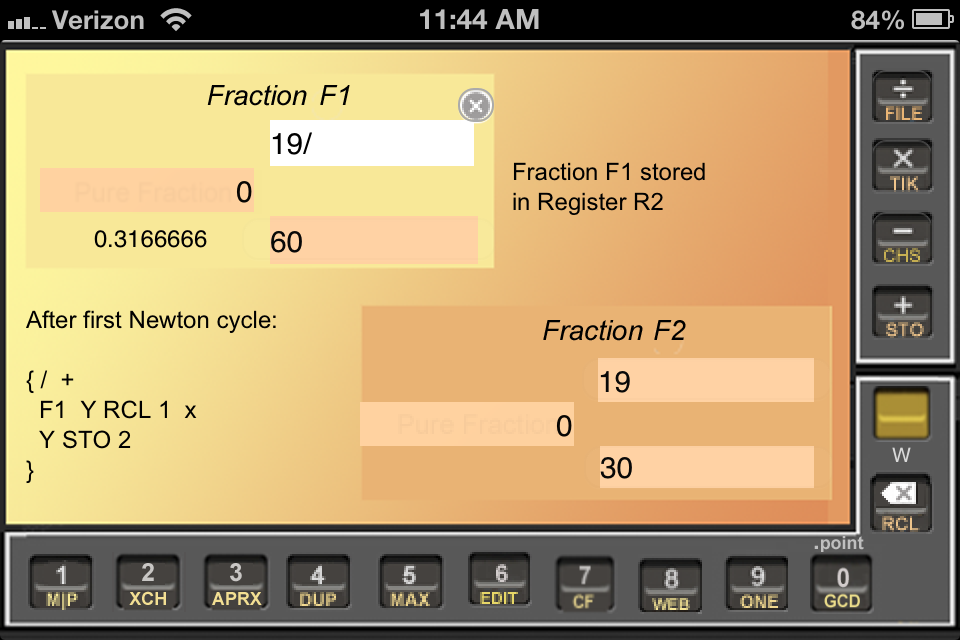
We can go again if you have time. Ready? First we have to restore the improved setup by restoring F2 from R3. Then we just repeat the exact same Newton steps, as indicated in Fig. WYW3. The results are different this time--better, actually--because the startup-guess is better: It is the once-improved version of the initial guess. The square of the twice-improved squareroot is 0.10000019--wow, that's good!
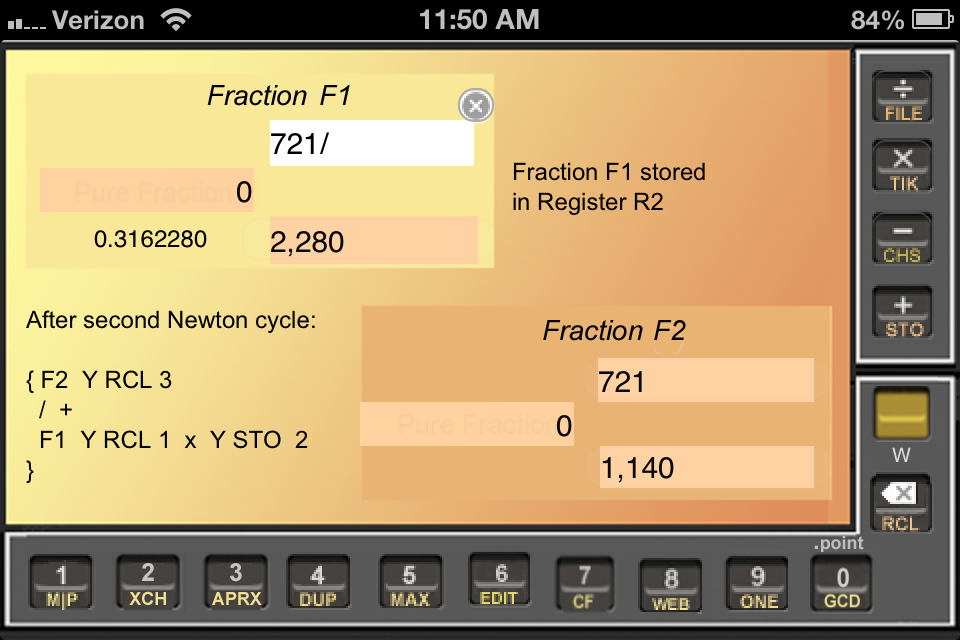
Let's go again. C'mon, it won't even take another minute. (Don't forget to start with { F2 Y RCL 3 } to get the target back into F2.) Fig. WYW4 shows the result.
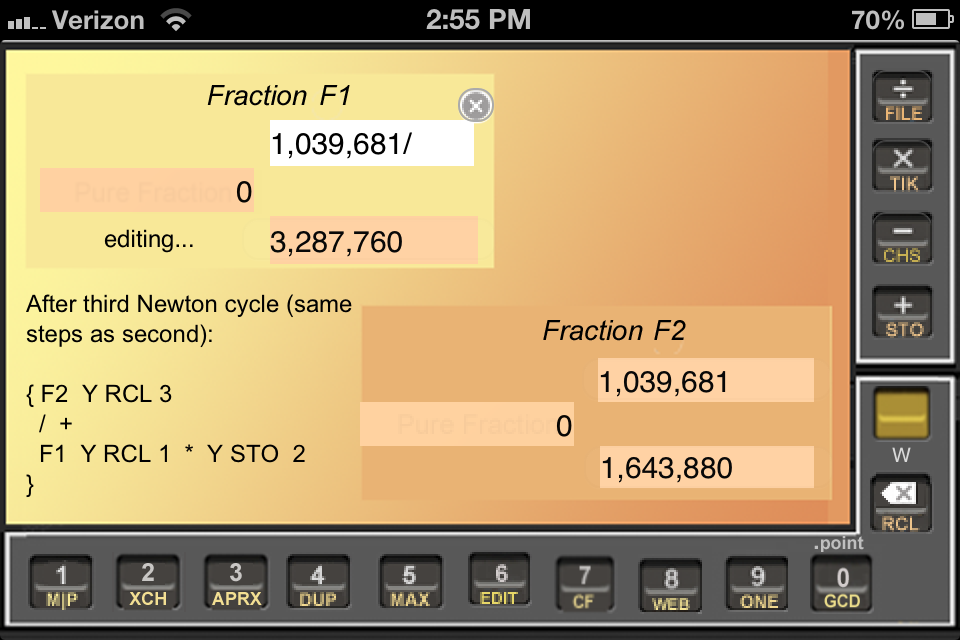
It's surprising, isn't it? how quickly the stacked numbers got large. As you get more experience, Frrraction will show that this is not an anomaly of any particular fraction problem, it is normal. It correlates loosely with increasing precision of the results as we go from one cycle to the next: It is the price of insisting upon exact results. That connection is fairly loose, as we discuss shortly. Nevertheless, it's clearly one of the reasons why decimal fractions are the workaday choice over the stacked forms.
If you try to check that result by doing { Y DUP F2 * } you get Fig. WYW5A. Numeric overflow occurred (because F1num*F1num is too large for Frrraction's 32 bit limitation). Even so, the decimal result is shown in F2flt (also called F2dec), correct to 7 digits accuracy.
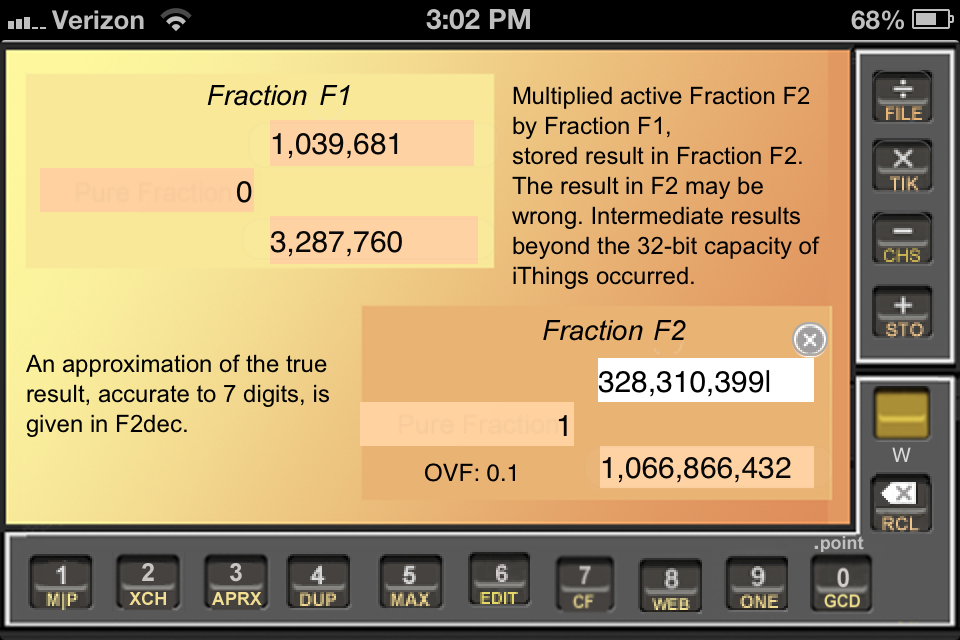
Actually, the square of our thrice-improved squareroot is 1,080,936,581,761 / 10,809,365,817,600 or about 0.100,000,000,000,093 as a decimal--which surely does equal 0.1 to 7 digits accuracy. (Because the squares of F1num and F1den are larger than pMAX, I had to use Frrraction's advanced high-precision hp( function to square that third approximation.) You can't get any better than 0.1000000 using 32-bit arithmetic. But, what happens if we ignore the overflow threat and try to improve upon the third Newton results by going around the Newton loop another time? Fig. WYW5B shows what you'll get:
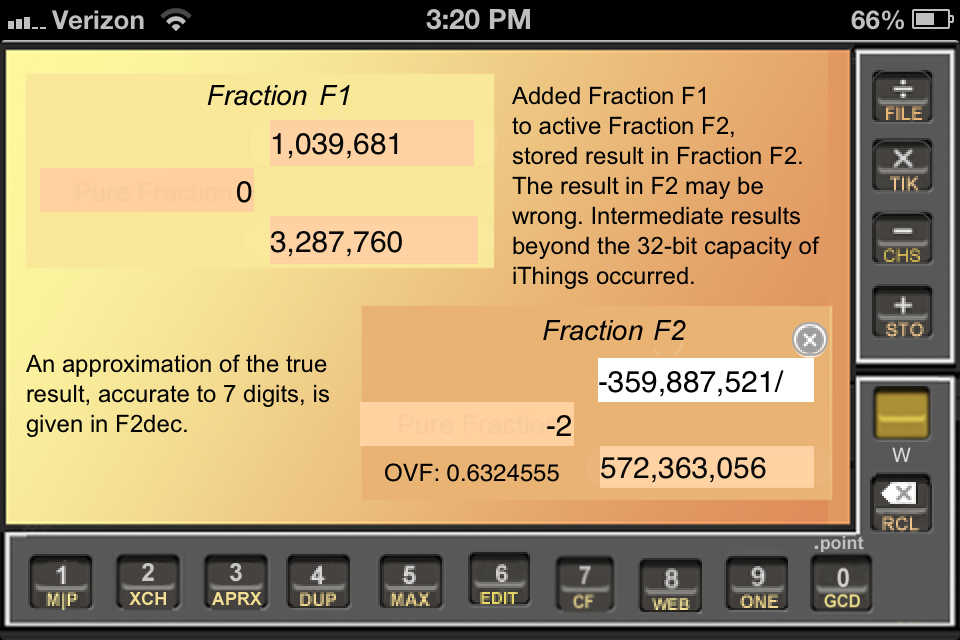
Oops, we only got partway through the fourth Newton cycle. Specifically, we did:
{ F2 Y RCL 3 / + }
The OVF note in F2flt indicates that adding F1 to F2 produced numeric overflow. As the Comment in the upper right of the screen explains, that means the calculation encountered numbers larger than the iPhone can handle. (This time the decimal result in F2flt accurate to 7 digits is of no use to us--we need the correct fraction in order to proceed from this intermediate step.) Often —but not always— overflow produces results like these that are clearly goofy: Adding two positives produced a negative??? That's clearly wrong. We've reached the end of the road towards the square root of 0.1. Surprise? Not really. We saw how fast the stack parts were growing with each improvement. Clearly, it wasn't going to be long before the numbers exceeded the 32-bit limits of the iPad, and it finally happened.
In the example above, you worked through finding the square root of 0.1 using Newton's method for finding the square root of some number—call it s for square—by improving an initial guess—call it g for guess. Next time, try it for a different number. And try the following improved setup to make it go a little more smoothly.
Set it up by storing s in F1 and R1, 1/2 in R3, and g in F2. These register assignments are rearranged from the previous section, and they make the Newton loop a bit easier to remember while doing it: Now we store F1 into R1 and recall R2 into F2 each time around.
After setup, repeat the following loop several times:
| Steps | Result |
|---|---|
| Loop | |
| F1 Y RCL 1 | get s from R1 into F1 |
| ÷ + | put s/g + g into F1 |
| F2 Y RCL 3 * Y STO 2 | view improved g in F2 |
| Repeat for accuracy | |
Here's a worked example for your first solo Newton job: Go for the square root of s = 3, using g = 2 as the first approximation. The sequence of g-values you should get in F2 and R2 is:
| Loop | #0 | #1 | #2 | #3 | #4 |
| g in F2: | 0 + 2/1 | 1 + 3/4 | 1 + 41/56 | 1 + 7,953/10,864 | 1 + 299,303,201/408,855,776 |
| — | 1.7500000 | 1.7321428 | 1.7320508 | 1.7320508 | |
| g2 in F1: | 3 + 1/2 | 3 + 1/16 | 3 + 1/3,136 | 3 + 1/118,026,496 | 0 + 2,081,377,281/2,125,448,192 |
| — | 3.0625000 | 3.0003188 | 3.0000000 | OVF: 3 |
I'm impressed: Since my college days I've been able at the drop of a hat to say that √2 is about 1.414 and √3 is about 1.732. What's impressive is that it only took 2 trips around the Newton Loop to find √3 ≅ 1.732 — whose square, 3.0003, is also correct to 4 digits.
Also notable about the power of the Newton method is that the result of Loop #3 around the Newton loop is accurate to all 8 digits that Frrraction can attain—and its square reproduces the target to all eight digits. Without going to high-precision arithmetic, it can't get better!
Do you wonder how I monitored the improvement in g2 to produce the bottom row of the above table? I did the following button-taps before proceeding back to the beginning of the Newton loop:
{ Y DUP F1 * }
If you try it yourself you will notice that you can't finish Newton Loop #5 due to overflow during the add-operation. It causes numeric overflow within Frrraction, producing junk in F1—so there's no point in continuing the procedure; the subsequent results would be based upon that incorrect result and would also be junk rather than an improved guess of the square root.
Next time, use your own choice of s and g. You'll know you're doing it right if the sequence of squared g-values gets closer and closer to s. A way to automatically see the g-values is to put a few more steps into the Newton loop, as shown below. Then each time around the loop, after squaring g by the "Y DUP *" combo, look at F1 to see if it's closer to s than the last time around the loop.| Steps | Result |
|---|---|
| Loop | |
| Y RCL 1 | recall s from R1 into F1 |
| / + | put (s/g + g) into F1 |
| F2 Y RCL 3 * Y STO 2 | put new g into F2 and R2 |
| Y DUP F1 * | view g2 ≅ s in FQ |
| Repeat for accuracy | |
Scroll up to review how we've been running Newton procedures by hand, tapping step by step to calculate square roots. After doing that a few times it starts to get tedious. That's where the CF Program Functions become really useful: After figuring out the step-by-step procedure, like in WYW KeytapCode1 above, you can automate it by doing cut-and-paste of the following code into an FrrrNote using Frrraction's EDIT (or just use the keypad within EDIT to enter the steps into an FrrrNote). Here's what it should look like:
| Newton Sqrt of s |
| target s in F1 and R1 |
| guess g in F2 and R2 |
| 1/2 in F3 |
| Run CF to improve g: |
| @<{{ F1 yRCL 1 / + |
| F2 yRCL 3 * ySTO 2 |
| yDUP F1 * |
| }}> |
| Display decimal value of g |
| @<{{ hp( get F2int |
| get F2den * |
| get F2num + |
| get F2den 00/ |
| 00put F2flt ) |
| @ }} |
| Look in Fraction F2 for g |
| and F1 for g^2 ~ s |
| then run CF to improve g |
After getting the function into FrrrNote, Return from the editor to Frrraction. Then set the Fractions and Registers to hold s, g, and 1/2. Then Tap the CF key once for each trip through the Newton improvement loop.
If you used the same target s = 3 and guess g = 2 as before, here's what you can now read from the Frrrmote at the end of the job:
Accurate to 18 decimal digits, the last value of g is 1+299,303,201/408,855,776, or 1. 732 050 807 568 877 295 ... and its square is 3. 000 000 000 000 000 005 ... You can get Frrraction to show you this by appending another CF function bracket to the above WYW CF Code 1:
| <{{ hp( get F2int get F2den |
| * get F2num + get F2den 00/ |
| dupX dupX 00* dupX 00put |
| F1intD = ) }} |
| {{ hp( get F2int get F2den |
| * get F2num + get F2den 00/ |
| dupX dupX 00* dupX 00put |
| F1intD = ) }} |
| X: 3. 000 000 000 000 000 005 |
| Y: 1. 732 050 807 568 877 295 |
| Z: 0 |
| T: 0 |
| U: 0 |