There are bridges between fractions and decimal fractions. One of them is a really powerful thing Frrraction can do with decimal numbers, but first let's discuss the ordinaries.
 background
background
CF is short for either "Classic Fraction" or — by far the more generally useful of the two — "Complex Function" a.k.a. "CFunction" — terms meant to distinguish them from Frrraction's built-in yellowkey Functions (+ - MAX EDIT etc.). CFs provide a way to effectively expand the collection of useable keys beyond the sixteen allowed by the limited space on the iPhone screen. The yellow PROG function key gives access to that expansion.
To use CFs, you Edit a FrrrNote to include one or more "CF Brackets" — matched pairs of braces enclosing code that defines the functions.
Within an hNote, the brackets look like this:
| CF | Bracket | entries |
|---|
| Egyptian Fraction |
{ a0; a1, a2, ... an } |
integer denominators |
| Continued Fraction |
[ a0; a1, a2, ... an ] |
integer quotients |
| CFunction |
{{ blah this that etc }} |
action keywords |
Egyptian Fractions and Continued Fractions are similar to each other, and simpler to use than CFunctions, so we discuss them here in HighSchool. Computer Programming is the true subject of Composite Functions so we discuss them in GraduateSchool.
There are two kinds of classic fractions: Continued Fractions and Egyptian Fractions. Continued Fractions are cool for a number of uses, including the secret codes my Grandson Galen and I are doing. Egyptian Fractions built the pyramids 4000 years ago. They're still good for figuring the best way to divvy things up, but aren't useful for much else any more.
An example Continued Fraction is:
5 + 1 / (4 + 1/ (3 + 1/ 2 )).
In normal notation, this continued fraction would be written something like this:
1
5 + ——————————————
1
4 + —————————
1
3 + ————
2
Continued Fraction Example 1
"Doing the arithmetic" (working up from the lower right) reduces it to the ordinary stacked fraction: 157/30.
Here's an example Egyptian Fraction:
5 + 1/4 + 1/3 + 1/2.
Doing its arithmetic reduces it to the ordinary stacked fraction: 73/12.
Classic Fractions are awkward to type, so Frrraction abbreviates them with a widely used shorthand bracket notation: Square brackets formed with the square braces [ and ] enclose Continued Fractions, and curly brackets formed with the curly braces { and } enclose Egyptian Fractions — look closely, those Egyptian curly braces are not the normal smooth parentheses.
The integer part of the fraction immediately follows the opening brace, and is followed by a semicolon.
If there is no integer part then the first entry within the bracket is 0 followed by a semicolon, viz. [0;a,b].
If the fraction has the mixed form a+0/1 i.e. there is nothing but an integer part then the bracket is simply [a;]. Don't omit the semicolon, though—without it, CF doesn't even recognize <[a] as a continued fraction command.
After the semicolon, the quotients (fraction parts) follow in order, each followed by a comma — although the final comma before the closing brace is usually omitted. For example, the continued fractions [5;4,3,2] and [5;4,3,2,] have integer part 5 and fraction parts 4, 3, and 2 and they equal 157/30.
YTapping Frrraction's EXEC key performs any of several tasks, depending upon what brackets you've put into frrrNote.
- If the current hNote contains an empty square bracket [] then EXEC causes the currently active Fraction to be converted to a Continued Fraction inside that bracket. (If there are several empty brackets, EXEC processes only the one that appears first in the hNote.)
- If, instead, frrrNote contains an empty curly bracket {} then EXEC converts the active Fraction into an Egyptian Fraction inside that bracket. (If there's a mixture of curly and square empty brackets, EXEC loads whichever appears first in the hNote.)
- If there's a loaded CF bracket prefixed with an Enable Code (OK, 'enable code' sounds fancy but it's just the <less-than symbol, or left angle-bracket) , such as <[5;4,3,2] or <{5;4,3,2} then the EXEC function "does the arithmetic" and puts the ordinary fraction into Frrraction's F1 or F2, whichever is currently the active fraction.
- If frrrNote contains no empty brackets and only normal loaded brackets without an enabler code—such as [5;4,3,2] or {5;4,3,2}—or contains no brackets at all, then the EXEC function has nothing to do and issues a complaint.
You don't really need the EXEC function in order to work with classic fractions, of course. You can use normal Frrraction arithmetic or just do the work by hand. Of course, you could wear itchy old hair shirts instead of soft cotton, too.
For example, to convert [5;4,3,2] into an ordinary fraction, the following steps (working from back to front) would do it:
- put 2 into F1
- put ONE into F2 then Divide
- put 3 into F2int (requires Frrraction showing Mixed Fractions)
- put ONE into F1 then Divide
- put 4 into F1int
- put ONE into F2 then Divide
- put 5 into F2int.
and there you have it: [5;4,3,2] is 5+7/30, or 157/30. (Frrraction's M|P function will convert the mixed fraction 5+7/30 into the pure fraction 157/30 if you don't want to do that chore by hand.)
Here's a procedure to go the other way — convert 157/30 into a continued fraction (writing the bracket down by hand as you go, I suppose):
- put 0+157/30 into F1
- Use M|P to convert it to 5+7/30
Now you know that the bracket begins with [5; ].
- Clear the 5 in F1int to 0
- put ONE into F2 and Divide.
This leaves 4+2/7 in
F2.
- The bracket continues as [5;4, ].
- Clear the 4 in F2int to 0
- put ONE into F1 and Divide.
This puts 3+1/2 into
F1.
- Put the 3 into the bracket as [5;4,3, ]
- Clear the 3 in F1int to 0
- put ONE into F2 and Divide.
This puts 2+0/1 into
F2.
- Put the 2 into the bracket as [5;4,3,2, ]
- Clear the 2 from F2int
This leaves the result as 0+0/1 or just zero, which says we're done. Delete the final comma in the bracket and the answer is complete: 157/30 = [5;4,3,2].
↑ to Frrr103 Menu
↑ to Main Menu
CF — Secret Code Ring
This is some really fun stuff! (in my humble opinion). If you can find a way to interpret the numbers in a Continued Fraction as letters of the alphabet, then the Continued Fraction becomes a message. And if you convert that Continued Fraction into an ordinary fraction, then the message is quite nicely disguised--especially to people who think numbers are just numbers!
I have been working with one way to interpret numbers as letters: The simple alphaNum code: Replace A by 1, B by 2, ... , and Z by 26. For better communication we extended the simple alphaNum code to include a number for a blank space, a period, and a question mark. We use 32 for space, 46 for . and 63 for ?.
That's all there is to it. Now [0;23,15,23,46] or 1/(23 + 1/(15 + 1/(23 + 1/46))) or 15931/367472 all contain the coded message "WOW." Cool, eh?
After you catch on, you can begin to let Frrraction do the heavy numeric lifting for you: Put the CF command <[0;23,15,23,46] into frrrNote (not forgetting the command arrow '<') and EXEC will put 15931/367472 into the active fraction. Notice that EXEC removes the Command Arrow to let you know it finished the job. Or go the other way: Put 15931/367472 into the active fraction and an empty square bracket [] into frrrNote and EXEC will fill the empty bracket for you, creating the loaded bracket [0;23,15,23,46].
There are two things to avoid:
- Don't end alphaNum-coded messages with the letter A, because A translates to 1 and by tradition Continued Fractions don't end with a one. That's because it would end in a thing like 23 + 1/1, which gets converted to 24 instead. In bracket form, a final 23,1] would get converted to 24]. The end of the message would change from WA into X. Not good.
It goes the other way just as well: If a continued fraction ended in anything but 1, say n + 1/15, this could be written as n + 1/(14 + 1/1) so its bracket then would end with n,14,1]. (This duplicity of terminal 1's is, by the way, the only way that the continued form of a fraction fails to be unique.)
- Don't try to make a long message into a single Continued Fraction. That's because when you convert a long Continued Fraction into a stacked fraction, the numerator and/or denominator of the stacked form can be HUGE, easily bigger than the iPhone's largest number 2147483647. This would cause Overflows in Frrraction when you use the EXEC function to convert between the stack and the continued form.
The solution of this problem is to break long messages into a series of short messages. These short messages are called "codewords" and a good length is four letters per codeword. Don't bother to try to match codeword boundaries to the actual word boundaries in your messages--let the punctuation characters sp . and ? do that job for you.
A typical long message: 16057/16558 28/451 69865/75672 2932/41465 362/1829 1663/1894. The first way I divided it into codewords, two of the codewords ended with A. In each case I just moved the A to the beginning of the next codeword. Those two five-letter codewords didn't cause overflow to occur so there was no other problem.
When you get tired of counting letters of the alphabet to get from messages to numbers, here is Frrraction to the rescue.
The CF Command that converts simpleAlpha to a normal Continued Fraction is: <[@ followed by the alphabetic letters of a codeword and the closing square bracket ]. Use PROG to put that into frrrNote, then employ the EXEC function. Bingo. frrrNote then contains the bracket form of the continued fraction.
For example, if you put <[@SHOW] into frrrNote, then the EXEC function will replace it by [@SHOW] <[0;19,8,15,23,]. So frrrNote would then contain a new CF Command, ready for EXEC to put the numeric continued fraction, which encodes the alphaNum SHOW message, into the active Fraction.
Frrraction can also go the other way: it can decode a stacked fraction that happens to be the alphaNum-encoded form of a text message: The CF Command in frrrNote is just [@] and Frrraction's EXEC function fills the empty bracket with the decoded form of the active fraction.
For example, if the active fraction contains 2791/53375 and [@] is in frrrNote then EXEC will replace [@] by [@SHOW]. If the active fraction was just a number, not an alphaNum-encoded message, what you would most likely get from EXEC is [@~~~~] because the tilde character ~ is what EXEC uses when it doesn't recognize a number as an alphaNum-encoded character.
The next step in Frrraction's Secret Message Codec facility is to use the much more powerful ASCII code instead of the overly simple alphaNum code. The only difference in operation is that the alphaASCII flag is the tilde character ~ rather than alphaNum's @ character. Thus, <[~Wow 012!] converts to [0;87,111,119,32,48,49,50,33,]. The stacked form of that particular numeric continued fraction happens to be so huge it generates an Overflow in Frrraction. The three-to-five character codeword limit applies to ASCII as well as to alphaNum. Breaking it up into two four-letter codewords we get [0;87,111,119,32] = 422831/36790106 and [0;48,49,50,33] = 80932/3886387.
ASCII is Page 1 of UTF8 and Unicode, the world's most important standard communication codes, so well worth being a little familiar with. For reference, here is a convenient list of ASCII codes. Good news is: You do not need to actually know ASCII in order to use it in Frrraction.
Decoding an ASCII-encoded fraction is just as easy: Put an empty ASCII-flagged bracket [~] into frrrNote and the active fraction will be decoded into the empty bracket. For example, if Fraction F2 were active and contained 80932/3886387, the empty bracket would be replaced by F2 = [0;48,49,50,33][~012!] — the numeric continued fraction followed by its ASCII-decoded form.
A final note: The two alpha encodings are mostly incompatible with each other — they share only the space, period, and question mark. I assume that, once you get to the ASCII [~ forms, you won't feel a need to turn back to the simple alphaNum [@ forms.
↑ to Frrr103 Menu
↑ to Main Menu
CF Example: Best Approximations
 background
background
Sometimes you have a fraction whose numbers are too large for the purpose at hand. For instance, maybe you think 177,215/15,979 is a good approximation of √123 but can't test it by simple multiplication in Frrraction because 1772152 overflows. Frrraction's APRX function provides an easy-to-use solution that you already know about — but classic continued fractions provide an unexpected, clever, do-it-yourself alternative.
Example: Suppose you want a simpler fraction (i.e. a fraction whose numerator and denominator are smaller integers) than 1,010/7,009 but with the same 7-digit decimal value. Putting 1,010/7,009 into Fraction F1 and ytapping D|F (Decimal-or-Fraction) puts the decimal form 0.1441004 into whichever is the active fCell in F1. APRX then finds the simpler fraction 712/4,941 which has the decimal form 0.14410038, which rounds to exactly match the seven digits of F1int. That might be a disappointing result, since 712 and 4941 aren't very much smaller than 1010 and 7009, but at least we know it's the best possible—if we want a simpler fraction we'll need to accept fewer than seven digits of precision.
Anyway, the whole point of this CF Example section of the guide is to show that CF continued fractions provide
an alternative way to find the most efficient fraction that represents any number in the range from 0.14410035 to 0.144100449, i.e. any number that rounds up or truncates down to the given seven digits. Here's how:
 |
Try it. Really.
Step 1: Put 0.14410035 —the smallest number that rounds up to match 0.1441004—into F1n and put an empty Continued Fraction bracket [] into frrrNote, then EXEC. This replaces the empty CF bracket by F1 = [0;6,1,15,1,1,3,1,3,8,1,...].
Step 2: Put 0.144100449 —the largest number that rounds down or truncates to match 0.1441004—into F1intD, put another empty bracket [] into frrrNote, and apply CF again. This replaces the empty bracket by [0;6,1,15,1,1,3,1,5,1,8,...].
Step 3: Make a new bracket by copying the previous two as far as they agree, producing [0;6,1,15,1,1,3,1,]. At the next entry, the two brackets disagree: the smaller has a 3, the larger has a 5. Complete your copy by using 1 plus the smaller, viz. 4, so it reads [0;6,1,15,1,1,3,1,4]. Convert that bracket into a command bracket by putting a <enabler in front of it, to obtain: <[0;6,1,15,1,1,3,1,4].
Step 4: Tap MAIN to exit the frrrNote editor, tap any F2-cell, and use the EXEC function. It will convert your command bracket into the active fraction 712/4,941. That's exactly the same as APRX got but it took a lot more effort on your part — isn't that just like a do-it-yourself job?! (APRX took less work on your part, but a whole lot more work on the computer's part!).
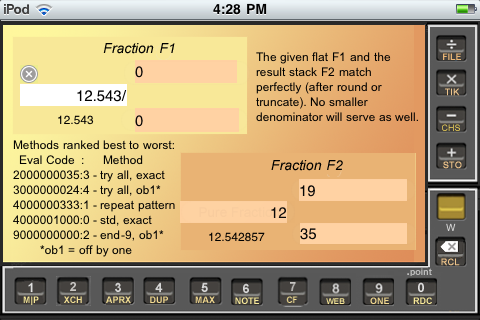
|
Fig. APRX2 summarizes the example. The frrrNote has been edited to include all three steps in one screen. Using frrraction's PROG function, I simply typed the lines "Best Approximation Example" and "1010/7009 = 0.1441004" after doubleclick-00 gave me the decimal value. The lines "F1 = ... = 0.144..." were produced from empty brackets by the CF-command in Step 1 and Step 2. The line "Lesser+1..." shows what's left of the CF-command-bracket <[0;6,1,15,1,1,3,1,4] after Step 3 collapsed it into F2.

Figure APRX2
A CF best-approximation example.
 |
Try it. Really.
For a second example, suppose you would be satisfied with a 4-digit approximation 0.1441 for that same fraction used above. Then the above steps become:
| Step 1: 0.14405 → [0;0;6,1,16,...] |
| Step 2: 0.1441499 → [0;0;6,1,14,...] |
| Step 3: <[0;6,1,15] |
| Step 4: → 16/111. |
As a check on the result of Step 4, put 0.1441 into F1int; with F1int still active, APRX then yields 16/111 in F2. It always works.
|
 |
Try more:
In the above examples we chose intervals to contain precisely all decimals that match (after rounding) a given decimal to a given number of digits.
The examples directly generalize to finding the most efficient fraction for a number required only to lie within a specified interval—any interval you want.
Here's a little series of problems asking for simplest n/d's in intervals. In each case find the unique fraction n/d, with smallest d which produces a decimal number in the specified range:
(a) between 0.123 and 0.456
[I guessed this one to be 1/4=0.25. I was wrong. What's the correct answer? Can you find an interval like these for which the correct answer would truly be 1/4?]
(b) between 0.123 and 0.246
(c) between 0.123 and 0.199
(d) between 0.123 and 0.165
(e) between 0.123 and 0.142857
(f) between 0.123 and 0.124999
(g) between 0.123 and 0.12306
The answers in reversed (g)-thru-(a) order are: 31/252, 8/65, 1/8, 1/7, 1/6, 1/5, 1/3.
|
This starter reference on best approximations explains in more detail.
↑ to Frrr103 Menu
↑ to Main Menu
Frrraction is a product of GRS Enterprises, NLC,
a Michigan company since 1978
Most recent update of this guide: November 26, 2021, 1415 GMT
Copyright © GRS Enterprises, NLC, 2010-2021
Not void, even where prohibited. Your mileage may vary.