
Oops. Doggone it.
Nobody but GoComics can use Calvin&Hobbes electronically.
No exceptions, they say.
Remember, Frrraction Actions can be quick or they can take as long as you want.
This Frrraction Action is to share with a friend who also has an iThing and the Frrraction app. With reference to CF — Secret Code Ring in Frrraction 104, you and your friend can send e-mails to each other that others can't read. If somebody intercepts your notes they'll just be mystified unless you give the secret away.

That would have been a swell cartoon to show in this section: Hobbes realizes they have a Secret Decoder Ring. "Wow!" Calvin says. "Ha!" he says. "Now Mom and Dad won't be able to understand us at all!" They think about that for a second, then Calvin says, "...not that they do anyway..."
Anyway, you can go see it at GoComics. (Use the Back button to return to this page.)
My last ASCII-coded words on the subject are:
1142725/85715688 , 389897/12480417 , 357172/11433185 , 1140086/115160201 , 47182/5474137
Hint: You can Copy-and-Paste from here into frrrNote. Then create a template in frrNote, something like
<{{ hp( NNN put f1n DDD etc. etc.
followed by an empty text bracket [~] and ... I've already said more than I intended. Go do it.
To do this Frrraction Action you need to know two things: (1) How to check to see whether two given numbers are reciprocals of each other, relative to a given modulus; and (2) How to use my two spiffy CF methods to find reciprocals of numbers (relative to a given modulus). Both are easy to do.
Example of (1): Use Frrraction to see if 3 is the reciprocal of 2 (mod 5).
Solution: We need to multiply 3 times 2, and divide the result by 5. If the remainder after that division were 1 then 3 would be congruent to 1/2 (mod 5). A quick way to do the arithmetic is to put 0+3/1 into F1 and 0+2/5 into F2 then multiply. In this case the product proves to be 0+6/5, which Frrraction immediately converts to quotient+remainder/5, or 1+1/5. The remainder is 1.
Conclusion: 3 and 2 are indeed reciprocals (mod 5).
TryIt:
Is 3 the reciprocal of 2 (mod 2147483647)?
Did you notice that you can check this one in your head? The integer-product of a residue and its reciprocal, before being reduced by the modulus, will always† be greater than the modulus—otherwise how could it end up being 1, smaller than one of the integers we multiplied?
†There's one (no pun intended) exception to this.
Example of (2): Determine the reciprocal of 100,000 (mod pMAX).
Solution: My favorite way to do this is the method based on continued fractions: Put 100,000 into F1num and yTap MAX (twice if necessary) to put pMAX into F1den. Clear F1int if it's not already 0. Then yTap EDIT and put an empty square bracket [] at the top of the frrrNote, tap ReturnToFrrr, and yTap CF to fill the empty bracket with the continued fraction of F1:
TryIt: What is the reciprocal of 100001 (mod 2147483647)?
<{{ hpArith(
) }}
then run the cf and confirm that F2den now contains 1.
If you need to be reminded how to multiply, divide, add, subtract two
NumDenInt fractionsYou can check out this webpage:
 ,
an elementary but very thorough and attractive introduction to fractions,
with links (at the bottom of that first page) to pages that expand on the topics
in this Appendix.
,
an elementary but very thorough and attractive introduction to fractions,
with links (at the bottom of that first page) to pages that expand on the topics
in this Appendix.
Here's a medium-level introduction to the arithmetic of residues.
The special numeric and quasi-numeric values that Frrraction handles with ease are:
Zero: Represented as 0 in the numerator, with any nonzero denominator.
Examples:
An interesting case is to divide something by Zero. What result should we expect?
| Try it:
Make F1 be 0/6, F2 be 1/4, then with active F2, /divide. Be sure to notice what Frrraction wrote in the H2den area (beneath F2int, beside F2den). While it's right there, UNDO then try multiplying the same two operands. It's what you expected, right? since (almost) anything multiplied by zero is zero. |
It might help to think of Zero as being a really tiny number — negative or positive — so tiny that multiplying any finite number by it yields another really tiny number, i.e. Zero. And putting that tiny tiny thing into the denominator would make the result be huge (see below).
Infinity: Represented as 0 in the denominator, with any nonzero numerator.
Examples:
To understand what to expect of arithmetic when one or both operands are infinite, think of Infinity as a huge positive or negative number but without any specific value; you can mentally think of doing the arithmetic with a variety of huge values and reasoning about whether the results would be always huge or always tiny or sometimes huge, sometimes tiny, depending on what particular huge values you think of.
A curious case to consider is the result of adding or subtracting two Infinities — the results could vary all over the place, right? If the two mental samples were almost equal, the result would be small; but if the two samples were far far apart — which could easily happen with two huge values — then the result could itself be huge. Mathematicians describe such outcomes-in-conflict as "indeterminate".
Signed infinities: Nevertheless, there is a valid arithme’tic distinction between huge positive numbers and huge negative numbers. Frrraction formalizes this distinction by maintaining Positive Infinity 1/0 and Negative Infinity -1/0 both notationally and arithmetically.
| Try it: Experiment with various combinations of ±1/0 in the fractions and the four arithme’tic ops, to see how Frrraction handles the sign-specific versions of infinity. |
Indeterminate: Represented as numerator and denominator both 0.
The one and only existing example: 0/0
Think of Indeterminate as being any value whatsoever, maybe huge, maybe tiny, positive or negative — an extreme case of why we use the adjective quasi when referring to these numbers.
To think about what to expect of arithmetic when one or both operands are indeterminate, think of doing the arithmetic with a variety of values—some huge, some small, some ordinary—and see how the results could vary widely, like what happens when you add a signed infinity to another (not necessarily the same sign) signed infinity.
Every computer stores data and moves data around in fixed chunks. Designed in the early 1950's, the University of Illinois' first computer used 30 bits. Common modern choices for this basic storage unit are one, two, four, or eight bytes. The storage unit for older computers and current small computers is usually four bytes (32 bits). Newer computers of desktop-class or larger store and transfer eight bytes (64 bits) at a time.
Apple iThings (iPhone, iPod touch, iPad) originally used four bytes but — since iPhone 5 — those mobile devices have migrated to 64 bits.
Frrraction's MAIN view is well served by the smaller 4-byte structure because it provides the user with direct interactive access to the numbers in six fCells while simultaneously providing explanatory information related to those numbers. That's quite a bit to fit on a mobile screen!
Frrraction's higher precision work is handled operationally by "hp" portions of user-created applets in frrrNotes, and s handled display-wise by the hShow panel in the upper-right quadrant of the screen.
The brain of each computer (its Central Processing Unit, or CPU) defines the natural number of bits for the integers the computer uses — including the numerators and denominators of Frrraction's rational number stacks. Any fixed choice of integer storage size places a limit on the magnitudes and precision of the numbers the computer can handle. It's true, software can be written to leverage that natural storage into larger amounts for some of its integers. The famous program called Mathematica uses such fancy techniques to attain unlimited number sizes and unlimited precision with no outside effort on the part of its users. Such provisions are not common, outside of special software for scientific applications.
To easily see the effect of storage size, consider having the storage size be a single nybble (4 bits, half of a byte). The sixteen distinct bit-patterns a nybble can exhibit can represent the sixteen integers in the range from -23 up to 23-1 i.e. -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, and 7.
There are many ways to associate bit-patterns with decimal numbers. One of the most popular, shown in the table below, is called "two's complement notation". The leftmost bit is 1 only for negative numbers. Changing the sign of a number involves more than flipping that sign-bit but there is a cute trick for doing it.
| binary | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| decimal | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Such a small range of numbers is useful for only a few specialized tasks. (The earliest microcomputers used the nybble, and were useful for controlling simple things like vending machines and clothes-washing machines.)
The 32 bits of the four-byte choice restrict integers to fall in the range between -231 and 231-1, i.e. nMAX = -2,147,483,648 and pMAX = 2,147,483,647.
(Yes, strange, isn't it? — in two's complement notation, negative integers can be a bit bigger than positives. Strange, but true. Count it up: There are pMAX positives plus pMAX+1 negatives plus 1 zero. That's
Bullseye: That's exactly the number of different bit patterns 32 bits can exhibit.)
A good way to visualize this limit is "the number line", which represents integers as equally-spaced dots on an infinitely long straight line, with 0 being in the middle in front of us; -1, -2, -3, etc. spaced further and further off the left; and 1, 2, 3, ... spaced off to the right.
Website  gives a graphic picture of the number line that should help you visualize it.
gives a graphic picture of the number line that should help you visualize it.
Arithmetic can be interpreted on this line: To add is to move to the right; adding 1 is to step one dot to the right; subtracting 1 is one step to the left; add 3 by stepping three units to the right; and so forth. The computer's four-byte limit discards everything to the left of -2,147,483,648 and everything to the right of 2,147,483,647.
 specifically visualizes addition and subtraction on the number line.
specifically visualizes addition and subtraction on the number line.
You can offer numbers outside that range to other fraction programs, or have them do arithmetic whose results would fall outside it, but — without doing anything to alert you — many other fraction programs simply get it wrong and go on as if nothing had gone awry.
To prevent that, Frrraction was designed to be on the lookout for all its internal operations where such mistakes could occur, and to alert you when they do. If your number-explorations are robust enough to push the iPhone limits, you will see the "OVF" overflow alerts from time to time—and an approximation accurate to seven digits is generally given in the Fdec cell of the active fraction where the incorrect result resides.
Key fact
32 bits limits decimal accuracy to about 7 digits.
Most computers use "floating point notation" to represent decimal numbers. With only four bytes to work with, older iThings could only directly achieve about 7 digits of accuracy. As Frrr103 said in this User Guide, digits beyond that are discarded by rounding and truncating. This "truncation error" implies uncertainty in the eighth digit of any decimal number.
Truncation uncertainty is usually just a mildly unpleasant fact of decimal life, but can sometimes be shocking. Here's a case that makes it look like a failure of both APRX and of the CF Best Approximation method:
With 1,001/3,001 in the F1 stack, GDC shows 0.33355548 in H1int. I misread that last digit '8' as '3' so 7 digits would be sufficiently accurate—I thought. Putting 0.3335554 into F1n and used APRX — I expected to get 1,001/3,001 in F1. Surprisingly what I got was 1,502/4,503 (see Fig. APRX3).
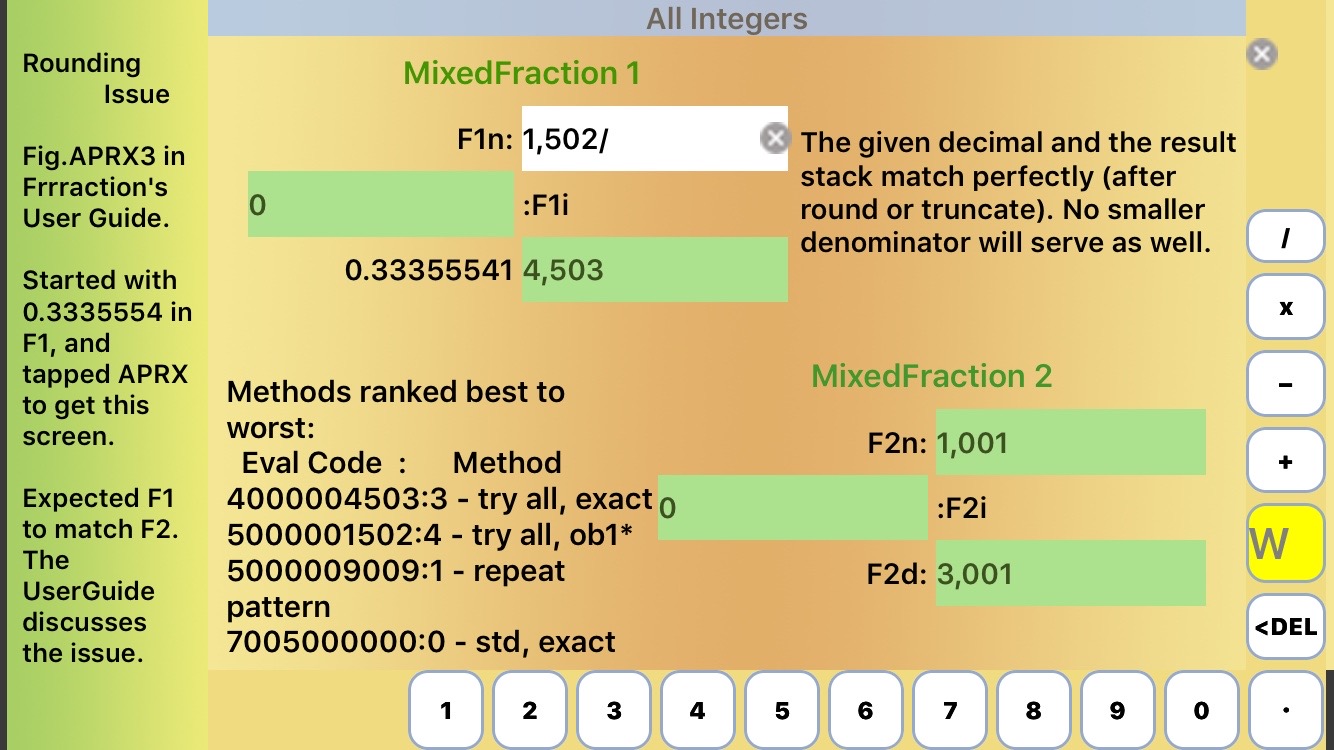
To investigate further, I tried the CF 4-step "Best Approximation" method on 0.3335554:
| Step 1: Put 0.333555535 into F1 (smallest decimal that rounds up to 0.3335554) and put empty bracket [] into frrrNote, then CF produced [0;2,1,499,1,4,1,1,12,1,2,1,2,1,4,3] in frrrNote |
| Step 2: Put 0.0.333555449 into F1 (largest decimal that rounds down to 0.3335554) and, leaving the prior result in frrrNote, append another [], then CF → [0;2,1,499,1,1,2,5,...] in frrrNote |
| Step 3: Append <[0;0;2,1,499,1,2] into frrrNote (a command bracket constructed to agree with both of the above brackets up to the first entry where they disagree, with last entry being 1 plus the smaller of the first disagreeing entries) |
| Step 4: CF → 1,502/4,503 as the best approximation of 0.3335554. |
That's no better than APRX — the same, in fact. But we know that 1,001/3,001 is better. Better than "the Best"??? What's going wrong?
Here's what happened: When GDC seemed to announce that 1,001/3,001 equals 0.33355543, I was the inadvertent victim of truncation error. The correct 8-digit value is really 0.33355548 because the correct 9-digit value is really 0.333555482.
(I found that out by putting this tiny Frrrapplet into frrrNote:
<{{ hp( get f1n get f1d 00/ sto 1 print/- < s>1-/ hShow ) }}
which produced:
0.3335554815061646117960679773408863712)
If we present APRX or CF's Best Approximation method with 0.3335555 then they both get the correct answer: 1,001/3,001.
Mystery solved!
There's one more ironic twist to this story. If you look closely at Fig. APRX3, you'll see that Method 4 seems to have come up with a denominator of 1,502, which suggests an answer even better than 1,001/3,001. APRX Method 4's results are always off by one, of course. If "off by one" from 0.3335554 meant 0.3335555 then once again we would seem to have a result better than "the Best". Again??? A little more work discovered that what APRX Method 4 actually found was 501/1,502 whose 8-digit decimal is 0.33355526. Thus "off by one" from 0.3335554 in this case meant 0.3335553. Another mystery solved.
(The way I found out what numerator APRX Method 4 had in mind with its 1,502–denominator was to give 0.3335553 to APRX, whereupon Method 3 found 501/1,502 as the exact match.)
The bizarre connection between decimal fractions and stacked fractions is well illustrated by this experience. Consider the summary in this table:
| Target | F1num | / | F1den | = | H1den |
|---|---|---|---|---|---|
| 0.3335553 | / | = | 0.33355526 | ||
| 0.3335554 | / | = | 0.33355541 | ||
| 0.3335555 | / | = | 0.33355548 |
Three consecutive targets — differing only in the least significant digit — yield three very different best approximations!
TryIt:
Such oddities may not be rare. See if you can find others like it.
Consider the stack 500/609 for starters.
Hint: Wolfram Alpha says its 9-digit decimal is 0.821018062.
What does Frrraction's GDC say about the decimal?
TryIt There are lots of things you can do with Frrraction to explore its four-byte limitation. Here's an eye-opener:
Make F1 be 2,147,483,647/1 (you can get that largest possible integer by tapping F1num then ytap MAX). (Remember, if you had wanted nMAX just ytap MAX twice—it alternates between pMAX and nMAX.) Then make F2 be 1/1 (for instance, tapping B|O|Z B|O|Z).
The sum should be 2,147,483,648, right?
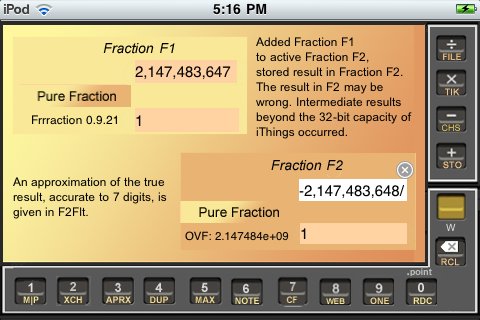
That's how Frrraction handled a result larger than pMAX. Interesting, eh?! OVF (overflow) is the computer jargon for that. When OVF occurs, Frrraction uses an alternative calculation to estimate the correct result, accurate to 7 significant digits, and shows it in the appropriate Hden cell, H2den in this case, where the estimate is 2.147484e+09. Frrraction also gives a brief explanation in the Comments section in the upper right corner of the screen.
Next experiment: What would you expect to get if you subtract 1/1 from that result, i.e. try to make the most negative possible number a little more negative?
Got a good guess? OK, try it:
Put -1 into F1 (the easy way is B|O|Z,B|O|Z,CHS), then +Add. Fig.BNE2 shows the result in F1.
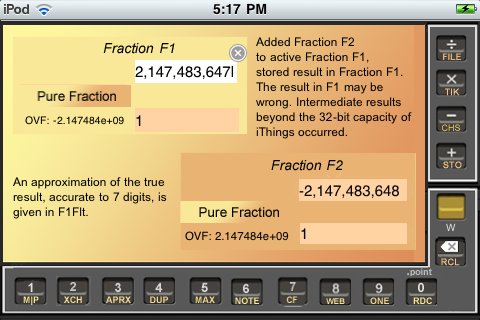
Hmmm, how does that new result make sense? It starts to make sense when you realize that the correct result should be -2,147,483,649 (or -2.147483e+09 accurate to seven digits in floating point notation, as seen in H1int in Fig. BNE2), and also realize that the correct result is geometrically to the left of the leftmost negative number that four bytes can put onto the number line.
A way to make sense of this is to consider that Frrraction converts the familiar number line into a "number circle": Think of 0 as being at the top of the circle; the other integers are equally spaced around the circle with 1, 2, 3, etc. curving around to the right and -1, -2, etc. curving around to the left from 0. The positives and negatives meet at the bottom of the circle, with 2,147,483,647 (half a unit to the right of the bottom) being the immediate neighbor of negative 2,147,483,648 which finds itself half-a-unit distance to the left of the bottom. Computer arithmetic adds 1 by stepping one position clockwise around the circle; subtracting moves counterclockwise. Isn't that clever?
For experiments with modular square roots—quadratic residues and qudratic nonresidues—these prime numbers will be handy for those who don't yet remember them all.
| 10^n | nearest Prime | mod4 | mod8 |
|---|---|---|---|
| 10 | 11 | 3 | 3 |
| 100 | 101 | 1 | 3 |
| 1,000 | 997 | 1 | 5 |
| 10,000 | 10,007 | 3 | 7 |
| 100,000 | 100,003 | 3 | 3 |
| 1,000,000 | 1,000,003 | 3 | 3 |
| 10,000,000 | 9,999,991 | 3 | 7 |
| 100,000,000 | 100,000,007 | 3 | 7 |
| 1,000,000,000 | 1,000,000,007 | 3 | 7 |
| - | 2,147,483,647 | 3 | 7 |
| 100,000,000,000 | 100,000,000,003 | 3 | 3 |
I included the peculiar entry in the billions because, as pMAX — iThings' biggest limitation — it's good to know that it is an odd prime congruent to 3 (mod 4), so -1 is a quadratic nonresidue, so the "non-existing" mSqrt of -1 can be the basis of the imaginary residues (mod pMAX).
That's all for now.