Menu of the Deep Dive
↑ to 'Deep' menu
Division Clusters — the deep dive
Gauss got the world started on modular division with his "euler units"†. He saw
that the collection of those particular units constitutes a special algebraic system that in later
generations came to be known as an (algebraic) group, the term coined by Everiste Galois.
† I call them that, Gauss probably just called them units.
An algebraic group is a collection G of objects (residues, say) with an operation (residue multiplication ⋅ say), with the key properties that
(1) if r and s are both in G then r⋅s is also in G;
(2) there is a unique member ω in G with the property that if r in G then
r⋅ω ≡ r;
and (3) Each r in G has an inverse r-1, also in G, such that
r⋅invr ≡ ω.
The group is abelian if r⋅s ≡ s⋅r
for all r, s in G.
All residue systems contain at least two groups — most contain more than two —
and the more important of those omnipresent groups consists of the euler units. The other is the trivial group {0,⋅} But those two are only the
tip of the iceberg, and units themselves are not the complete division story: For that, we need to examine division clusters of residues — they're all important and they're not all groups!
↑ to 'Deep' menu
Definition of the key: division clusters
Division Cluster Cr of system Zm consists of the residues s whose
greatest common divisor with m is the same: gcd(s, m)=gcd(r, m).
There is a one-to-one correspondence between division clusters and
euclidean integer divisors of the modulus m.
The mod-m residue and euclidean integer
cr = gcd(r, m) is called the center of the cluster,
and is the only member of Cr that divides m.
We already met two of the clusters: C1 is Gauss's group of euler units, and Cm —the cluster consisting solely of the residue 0. Those are the only clusters that exist in every residue system.
Example Z12: The clusters for modulus m=12, showing centers as C-subscripts
and ω-values emphasized, are:
C1={1, 5, 7, 11}e,
C2={2, 10}i,
C4={4, 8}u,
C3={3, 9}u,
C6={6}i, and C12={0}u.
We sometimes call the clusters "modal" because of their
central connection — directly via their "centers" — with the structure
of the underlying system modulus.
A correct but inefficient computational method for generating a list of a
cluster's members derives directly from the definition:
Cr is the set cr ⋅ C1
obtained by multiplying cr by each euler unit.
The method is inefficient because it generates each member of the cluster multiple times. Notice in the
Z12 example, for instance, that C1 has twice as many members as C3: There
are not enough residues in any of the clusters except
C1.
We address this more specifically as a division issue in due course. In the meantime we can see the
numerical extent of the inefficiencies by counting the number of members of the various clusters as follows.
The number |C1| of residues in C1 is calculated
using the totient function φ(m) later named Euler's Phi function. If
cr ≠ 1
then the size of C1 is
always a multiple of
|Cr| — the multiple is almost always by 2 or more, the only exceptions occurring when 2 is a residual unit and |C2|=|C1|. Using Euler's totient function again,
the size of Cr is
|Cr| = φ(m .÷. cr).
It's worth noting that if cs > cr and if Cs and Cr are on the same trace with Cs being farther along the trace towards Cm then again
|Cs| ≤ |Cr| with |Cr| being an integer multiple ≥2 larger — even though φ(m) is
itself not monotonic.
Anyway, |C1| is larger than |Cr| by the factor
φ(m) .÷. φ(m .÷. cr).
↑ to 'Deep' menu
Clusters and Chinese Cubes
A Chinese Cube for Zm is actually a "hyper-rectangle in euclidean integer
n-space where n is the number of distinct prime divisors of m" — but
"cube" is so much easier to say. Such cubes provide excellent displays of Zm
when n≤3. Here's the cube for Z36:
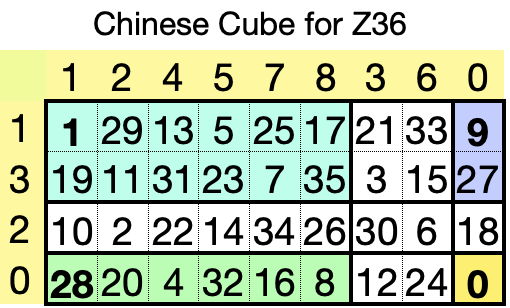
Units colored, Omes
bold, Ints white
The nine clusters of Z
36 — one cluster for each distinct integer divisor of
m — are outlined in the figure with thick lines, and the group identities of the
four unit clusters are shown in bold font. Note that the number of maximal prime-power factors of
m=36 is
n=2 — always the same as the number of prime divisors of
m
— so the
n-dimensional hypercube is a simple 2-dimensional rectangle.
The two maximal prime-power factors of 36 are 2
2 and 3
2; in
this example
the system Z
4 for one of those factors provides the row labels of the cube and
similarly Z
9 provides the column labels. Those labels are themselves
1-dimensional Chinese Cubes —
i.e. each is a single straight line — and their residues are listed in this order:
euler units first,
then the residual
ints in the
prime-power stack in ascending exponent order, and finally the residual
unit at the top of the power
stack.
Each of the 36 residues of Z
36 has its unique place in the cube — the locations
are precisely
specified by the Chinese Remainder Theorem, in terms of the row and column labels. Residue
r (mod 36)
belongs in the row given by the remainder r (mod 4) and column given by r (mod 9).
e.g. 34 is in the row labeled 2 (mod 4) and column labeled 7 (mod 9).
Because the orderings
of those labels reflect the divisibility structures of the single-factor systems Z
4
and
Z
9, the resulting 2-cube strongly reflects the divisibility structure of Z
36.
Because of the row and column ordering, the euler units are all at the upper left,
occupying some of the lefthand edge and some of the top edge of the cube; the cluster of units
with
identity 9 — together with all the other clusters whose residues it can divide —
occupies the
entire righthand edge; the cluster of units with identity ω=28 — and all the clusters
of residues
its members can divide — occupies all of the bottom edge; and — also as
always — C
m={0} is at the bottom right corner.
Almost as important as clusters are their "traces": The trace Tr of
division cluster Cr is the collection of all residues t of the form
t ≡ x ⋅ s where x is any member of
Cr and s is any residue modulo m.
The trace of a cluster contains all the residues of the cluster and usually more.
The trace of a cluster is important because it
turns out to be the complete set of all residues that can be divided in a broad sense♦ by the residues of
the cluster.
With reference to 2-dimensional Chinese CUbe graphics, the closest boxes in the trace of a given
box are: the neigboring box just below and the neighboring box just to the right of the given box.
The trace continues, always down and to the right of each box in the trace, ending with the 0-cluster
at the bottom-right corner. Summary, good for any number of dimensions: The given box is in
its own trace; and for each box in the trace, all neighboring boxes that are closer to the 0-box are
in the trace.
♦ That's true "in a broad sense", but the best version of division — (i;u)-division — breaks the trace of a cluster of pure residual integers with center c into three parts:
ƒ
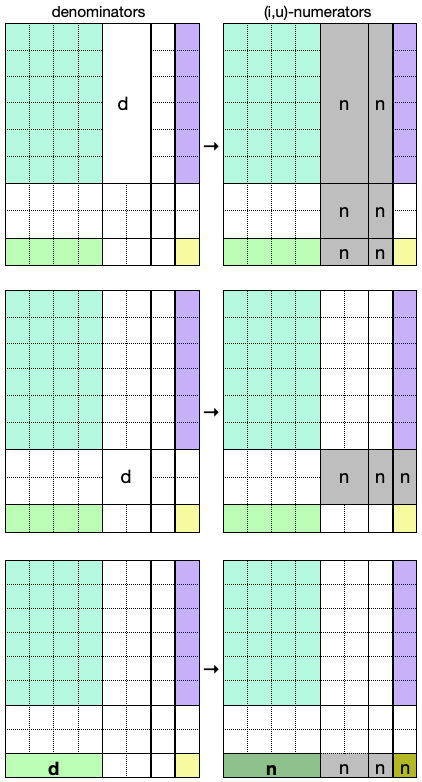
Traces — modified for (i,u) — shown darkened
First, the power stack of clusters with centers from c1 up to and
including ck-1 where ck is the center of
the unit cluster at the top of that power stack of integer clusters;
Second, the entire face of the particular Chinese cube which contains that particular unit cluster and includes its merger with all the other integer traces of the residue system; and
Third, the region where the first part of the trace merges with all the other integer-or-unit traces.
The first part of the trace is divisible by the particular integers in question, and the second part only by the top-of-stack units along with all other integer clusters. This part contains pure integer clusters and mixed integer×unit clusters, but no pure unit clusters.
Uniquely, the
trace T1 of the group of euler units contains every residue in the modulo-m
system—that's why euler units can divide every residue in the system.
A handy test of whether any given residue is divisible by the members of a given cluster is:
If r is a unit then residue x is in Tr if and only if
ωr ⋅ x ≡ x
(mod m).
Curiously, the product ωr ⋅ x
is always in Tr regardless of whether or not x is in Tr.
If r is not a unit then residue x is in Tr if and only if
cr euclidean divides cx. That is to say, gcd(r,m) .|. gcd(x,m).
Example traces:
For modulus 12 the traces of the clusters are:
T1={all the residues mod m},
T2={2, 4, 6, 8, 10, 0},
T4={4, 8, 0},
T3={3, 6, 9, 0},
T6={6, 0}, and
T12={0}.
The shadow of
a cluster contains just "the usually more", i.e. members of the cluster's trace that are not in the cluster.
The list of shadows might clarify discussion of traces by omitting the duplication.
Example shadows:
For modulus 12 the shadows of the clusters are:
S1={all residues except those in C1},
S2={4, 6, 8, 0},
S4={0},
S3={6, 0},
S6={0}}, and
S12=Φ (the empty set).
↑ to 'Deep' menu
Definition: units
From the perspective of modular division there are two distinct kinds of residues: units and
integers — or three kinds if we count mixes.
Residual units are the residues whose division cluster is an algebraic group.
We use the adjectives "modular" or "residual" in contexts that might confuse these units
with eulers or with euclidean integer units.
It follows from the definition that residual units have inverses, and each kind of unit has
its own group identity
ω to fit its role in u⋅u-1≡ ω and
ω/u ≡ u-1. This
allows them to play roles similar to the euler units (whose identity is ω = 1).
Gauss's definition of modular division using
euler units applies with one small change to all units. We spell it out here:
* Modular Division by any unit:
We start the derivation the same as for euler units: Let the quotient n/d
(equivalently n ÷ d)
be some residue q, where d is any
residual unit. Following Gauss, we define the quotient q to be n⋅d -1.
This almost satisfies the fundamental division requirement that
d⋅q ≡ n. Instead, it yields
d⋅q ≡ d⋅(n⋅d -1)
≡ n⋅(d⋅d -1)
≡ n⋅ωd.
What it takes to close the deal is for
n⋅ω
d to be
congruent to the numerator
n. The way
we choose to accomplish that is to simply impose it as the condition for divisibility
of
n by
d:
By definition, d | n (i.e.
unit denominator d
divides numerator n)
if and only if
n ⋅ ωd ≡ n.
(Note, the divisibility condition is
automatically satisfied if d is an euler unit.),
Is residue r a residual unit (mod m)? An easy test:
r is a unit if and only if gcd(r, m) ≡ gcd(r2, m).
Example: gcd(16,72)=gcd(256,72)=8 so 16 is a residual unit in the cluster C8.
Example: gcd(14,72)=2 ≠ gcd(196,72)=4 so residues in cluster C2 are not
units.
Example: gcd(72,72)=gcd(5184,72)=72 so residue 72 is a residual unit in cluster C72.
How calculate the inverse and the omega of a residual unit u?
Calculate the successive powers u, u2, u3, …
until the first time uk ≡ u for some euclidean
integer k > 1
which occurs if and only if u is a residual unit.
Then ωu is uk-1 and the
inverse u-1 is uk-2.
Example: The power sequence for 16 (mod 72) is 16, 40, 64, 16 so k = 4,
ω16 ≡ 64, and 16-1 ≡ 40.
Easily confirm by calculating u⋅u-1≡16⋅16-1≡16⋅40≡ 64 ≡ ω16.
Other methods require computing the prime factorization of the modulus. It is a benefit that
the above algorithm does not.
↑ to 'Deep' menu
Applications of modular division by units
1. 16⋅x≡56 (mod 72), x=?
Solution: ω16≡64 and 64⋅56≡56 so 16 | 56.
Thus x≡56/16≡56⋅40≡8.
Confirm: 16⋅8≡56? yes.
2. 16⋅x≡58 (mod 72), x=?
ω16⋅ 58 ≡32≠58 so 16 does not divide 58,
the quotient 58/16 is undefined, and 58⋅16-1 is meaningless.
3. 5⋅
x ≡549 (mod 551), x=?
Solution: 5 is an euler unit so it does divide 549,
and 5-1≡441 so x≡441⋅549≡220.
Confirm: 5⋅220≡549? yes.
This congruence had only one solution because the denominator 5 was euler (mod 551).
4. 5⋅
x2 ≡549⋅
x (mod 551), x=?
Comparing this with the preceding example it is clear that x=0 and x=220 should
both be solutions; not so clear is that there are other solutions as well
... and if euler units were the whole story of units, there would be just two.
In problems like this there's always the possibility of one solution in each division cluster.
This modulus is the product of two simple primes (551=19⋅29) so there
are four clusters, each consisting entirely of units: C1,
C19, C29, and C551.
Multiplying the congruence through by the not-yet-known inverse of x yields:
5⋅x ≡ 549⋅ωx
which is one equation and one obscure relation and two unknowns.
We don't know x yet, but we do know that its omega is one
or another
of ω1=1, ω19=494, ω29=58,
ω0=0. We can assume those ω-values one at a time,
solve for x, then reject x
if it is in the wrong cluster i.e. has the wrong omega.
For instance, if we assume x is in C19 then the congruence
to solve is
5⋅x ≡ 549⋅494 ≡ 114,
which yields
x=114/5≡133; 133 is in C19 so 133 is a solution.
Assuming C29 yields x ≡ 87, C1
yields x ≡ 220, and C551 naturally yields x ≡ 0 :-)
Complete quadratic equations,
a⋅
x2+
b⋅
x+
c ≡ 0 (mod
m),
even with only a single unknown, are an order of magnitude more difficult than the above examples.
If we multiply through by
x-1 what remains is still quadratic:
a⋅
x+
b⋅ω
x+
c⋅
x-1 ≡ 0,
so it doesn't help.
There are some special cases where I can see how to proceed. The most obvious case is when the integer
discriminant
disc=
b2-4ac is an integer square, where we can adapt the quadratic formula to the
modular problem. For example:
5.
x2+
x−12 ≡ 0 (any modulus)
The euclidean integer discriminant b2−4ac=49=7⋅7 so
it is a square and euclidean integer solutions exist. They are x = (−1±7) / 2 = 3 or −4. Amazingly, those two are among the solutions for all residue systems!
Translated into modulo 72, for example, the congruence to be solved is:
x2+x+60 ≡ 0 (mod 72),
and its complete list of solutions is:
x≡3 in C3, 12 in
C12, 59 in C1, and 68 in C4.
Of course x ≡ 3 and 68 (≡−4) are shared with the
euclidean case so they were expected, but...
...where did 12 and 59 come from? Example 6 answers that.
After considering a derivation
of the modular quadratic formula it's a surprise that
the quadratic formula found any solutions at all!
We discuss "Example 5" issues further after considering division by non-units.
The next example is one where the integer discriminant
b2 − 4
ac
is not an integer square — but the
modular discriminant
b2 − 4
ac (mod 663) is a
modular square — so: blindly applying the quadratic formula might still work on the modular problem.
6.
x2+26
x−17 ≡ 0 (mod
663) (663=3⋅13⋅17.)
The discriminants are disc = 744 (int) ≡ 81 (mod 663). 744 is not square,
so the euclidean integer version has no (euclidean integer) solutions but, taking the quadratic formula
x = (−b ± √(b2−4ac))/2a
literally, while calculating it as modular arithmetic, yields
x ≡ (-26 ± 9) / 2 ≡ 314 and 323
— a partial success.
The actual complete list of modular solutions is: x ≡
119 in C17, 314 in C1, 323 in C17,
and 518 in C1. We expected 314 and 323 but where did the other two
come from?
Answer: We thoughtlessly took √81 to be simply ±9, but Z663 contains those along with
±264 as the four
square roots of 81 (mod 663) — all four are in C3. They produce the unexpected extra
solutions for Example 6.
The same observation serves for Example 5 as well.
The next example is one where neither the integer discriminant nor the modular discriminant is square,
but the quadratic equation still has solutions.
7. [haven't found an example yet, nor proven that none exist —
here's how close we've gotten.]
Summary
Applications of modular division by residual units leave much to be explored, but that kind of
modular division itself is in pretty good shape. If the prime factorization of a modulus contains
nothing but distinct primes then all the residues in the corresponding residue system are residual
units. If any repeated factors occur then the residue system also contains residual integers,
which are a different kind of animal.
↑ to 'Deep' menu
Definition: non-units
Residue r is not a residual unit if r2 is not in the same residual
cluster Cr as r. The most distinctive alternative is that r might be
a residual integer. The other possibility is that r is mixed — the product of a residual integer
times a unit that is non-euler.
residual integers are quite unlike units: They have no inverses — and their
clusters don't have any omegas so there's not even anything to base a notion of inverses on.
In division they behave much more like euclidean integers: Specifically, suppose you keep dividing by the same
residue r in a division sequence like
s0,
s1 ≡ s0 / r,
s2 ≡ s1 / r,
s3 ≡ s2 / r, …
When r is a residual integer the sequence usually terminates
at some sk which r cannot divide. When r is either kind of unit, residual or euler,
the sequence never reaches such a stopping point: it eventually enters a repetitive
cycle of units.
Divisibility in general: A simple rule we are about to explore is: Unit or integer, residue r is able to divide residue s
if and only if the center cr divides the center
cs with 0 remainder (using the euclidean algorithm '.÷.' for integer division).
Finding all quotients — all solutions, that is, of the division-defining congruence d⋅ q ≡ n
(mod m) —
is the other main key to modular division
q ≡ n / d :
If d not.|. n, i.e. d does not divide n — which is to say, the center cd
does not euclidean divide the center cn — then there are no solutions of the
original congruence.
Otherwise, the trick to finding all "quotients" is to use euclidean integer division to remove the common factors
cd = gcd(d,m)
from both sides of the congruence. This reduces d⋅ q ≡ n
(mod m) to
ed ⋅ q ≡ n .÷. cd (mod μ)
where ed = d .÷. cd is an euler and
μ = m .÷. cd is a smaller modulus.
We know ed
is an euler unit since it results from removing all the prime factors that d shared with m.
Since euler units divide all residues, ed modular-divides n
as well as it modular-divides n .÷. cd and division by that euler unit provides
a first solution — a "starter quotient" — call it qo where:
qo ≡
ed-1 ⋅ (n .÷. cd)
(mod μ).
Since i⋅μ is congruent to 0 (mod μ) but not 0 (mod m) until i
reaches cd,
we see that the set
qoΔμ = { qo + i⋅μ
for i = 0,1,..., cd -1} (mod m)
provides the complete set of quotients modulo m.
The divisibility condition necessary and sufficient to guarantee
the existence of solutions q for d⋅q ≡ n (mod m) was shown
to be simply that the center of Cd must divide the center of Cn.
It was also shown that the number of distinct solutions is cd so, unless
cd is 1 — meaning, unless d is an euler unit — then the
quotients that exist are not unique.
Example divisibility: Residue 58 divides 56 (mod 72), but 58 does not divide 69. That's because
c58=2, c56=8 and 2 .|. 8, but c69=3 and 2 does not
euclidean divide 3 (the euclidean remainder of 3 .÷. 2 is 1, not 0).
As intended, this shows that not every residue can divide every residue.
Example uniqueness: 58/17 ≡ 50 (mod 72) and quotient 50 is uniquely
defined — there is no residue except q ≡ 50 that satisfies the congruence
17⋅q ≡ 58 (mod 72) — which is because 17 is an euler. On the other hand,
58/50 presents an issue: x=17Δ36 so x=17 and x=53 both satisfy the defining
congruence
50⋅x ≡ 58 (mod 72) and they can't both be the quotient. We need
some rational way to reject all but one of the alternative quotients, something along the lines of
Euclid's requirement that the remainders of his divisions must fall between 0 and the diminished
denominator. But, wait...
Uniqueness achieved!
The ambiguity originates with euler units that are transparent to the center of the denominator; the culprits are the euler solutions of the congruence cd⋅e ≡ cd.
There is a direct remedy: Organize the division algorithm to form qo
as n⋅(ed)-1, then form the full quotient as q .=. (qo .÷. cd).
Since cd divides cn, the particular aspect of cd that makes the ambiguity invisible in d is also present
in cn and — with this proposed organization of the calculation — it still remains present in qo because it hasn't yet been removed by
the euclidean division of cn by cd.
Postpone the congruence solution examples,
later adapt them from c,e to i,u
Our approach to extending modular division into non-unit denominators entails factoring the
operands — but not into anything like prime factors. There are many factorizations of residues into
products of other residues but
two in particular stand out in importance: the (c;e)-factorization and the (i;u)-factorization.
All residues admit both.
One of those factorizations was the basis for the preceding introduction to modular division, and we
formalize it here:
The (c;e)-factorization of residue r expresses it as the product
r ≡ cr⋅e
of the center cr of its cluster times an euler unit e.
The c and e of (c;e) are just multiplied to produce r but we use
the semicolon ';' instead of the center-dot '⋅' because (c;e) is an ordered pair: As products
(c⋅e) and (e⋅c) are the same
but as factorizations (c;e) is not the same as (e;c) — the center
is always mentioned first.
The center is of course unique, but the euler factor is not. The number of distinct alternatives for the
euler can be calculated using the Euler Phi function as
|cr;er| = |C1| .÷. |Cr|.
The list of residues to choose those eulers from is of length cr, often more than
|cr;er|.
Calculating the "c" of the (c;e) factorization of any residue r is easy: cr is simply
the greatest common divisor gcd(r,m).
The euler factor is a bit trickier.
Define eo = r .÷. cr and
δ = m .÷. cr.
Then (c;e)'s euler factors must be selected as any euler member of the
set eoΔδ which is shorthand for
{e=eo+i⋅δ ∀ integers i=0, 1, 2,..., cr-1}.
Notice, the number of quotients to choose from is cr, but the number of eulers to
choose is
|cr;er| = |C1| .÷. |Cr|,
which is often less than cr.
Example (c;e) mod 72
48 ≡ 24⋅5.
Another example (c;e) mod 72
48 ≡ 24⋅11.
OK, the whole example with c48=24, eo .=. 2,
δ .=. 3, and |c48;e48| .=. 12
2Δ3 = {2 5 8 11 14 17 20 23 26 29 32 35 38 41 44 47 50 53 56 59 62 65 68 71}
whose euler subset is {5 11 17 23 29 35 41 47 53 59 65 71}
so (c48;e48) ≡ 24⋅{5 11 17 23 29 35 41 47 53 59 65 71} —
a far cry from being unique!
The modular "(c;e)-quotient"
Early version: To divide n by d we euclidean-divide cn by cd
to get the core factor cq of the quotient; then
we unit-divide en by ed
to get the euler factor eq of the quotient — or we can do eulers first then centers,
it makes no difference. Multiplying the (c;e) factors yields
the quotient q ≡ cq⋅eq.
Unique quotients version: To divide n by d first (c;e)-factor d and multiply
n by the euler inverse ed-1 to get qo; then euclidean divide qo
by cd to get q.
The "early" version guarantees that q ≡ n / d exists, but
the "uniqueness" version guarantees the quotient is unique since
the choice of eulers no longer affects the quotient.
But wait... again...
...there is yet another way for (c,e)-division to go wrong — and this fault blows (c;e) out of the water: Sometimes the euler factor, as calculated by the euclidean division e = r .÷. cr , turns out not to be an euler! but (c;e) depends upon euler which enables it to divide any numerator.
Example 'e' not an euler — Consider two residues modulo 360:
r1 = 104 ≡ (c,e):8⋅13.
r2 = 208 ≡ (c,e):8⋅26.
The e-factor 13 of r1 is truly an euler unit, but that factor 26 of r2 is a residual integer. The prime factorizations of m and of the two residues is revealing:
m = 23⋅32⋅5
r1 = 23⋅13 and
r2 = 24⋅13.
The exponent of prime 2 in m is k = 3, in r1 it is j1 = 3, and in r2 it is j2 = 4.
The fact that j2 exceeds k is the problem: The exponent of any prime p in the center c of the cluster the unit shares with other units will always match that prime's exponent k in m, even when the exponent in the unit exceeds k, as j2 does in r2.
The result is that the excess exponent i = j−k will always get transferred to what was supposed to be the euler factor in a (c;e)-factorization.
We tried moving such excess unit-factors back into c where they belong, but the result is that the enlarged value of c in a denominator may no longer divide its counterpart in the numerator — even when numerator and denominator are in the same division cluster!.
Unless a solution is discovered, (c;e)-division must be (as Apple's Xcode would put it) deprecated.
Move "Intro to q<>d" somewhere below (see Example q,d-symmetry)
The deprecated (c;e)-division has another peculiarity: It makes no reference to residual units! We're not that sad to see it be forced out.
Maybe this next factorization is better? Focussing directly upon the interplay between residual integers and residual units, it surely seems more fundamental.
(i;u)-factorization expresses r as
r ≡ ir⋅ur where ir
is a residual integer and ur is a unit.
The "integer factor of r" is 1 if r is just a unit; otherwise ir is
a unique residual integer; in either case, a starter value for "the unit factor of r" is extracted from r
by the euclidean integer division uro = r .÷. ir.
The number of distinct alternative units for r is simply
|ir;ur|=ir itself. The
complete list of
those alternative units is uroΔ(m .÷. ir).
Note, the reason this works is:
ir ⋅ (m .÷. ir) = m ≡ 0.
Calculating the integer factor i of the (i;u) factorization is the tricky part. It is easy enough if we can use the prime factorizations of the modulus and its residues —
easy enough for modest systems with modulus in the billions, but virtually impossible when the modulus
is huge. Our method does not need any prime factorizations.
Example (i;u) mod 72
48 ≡iu: 3⋅16.
The integer part of the unit u48 is 1 of course, 16 ≡iu 1⋅16
as is the unit part of the integer i48, 3 ≡iu 3⋅1)
Another Example (i;u) mod 72
48 ≡iu 3⋅40.
OK, all the alternatives
48 ≡iu 3⋅(16Δ24) ≡ 3⋅{16, 40, 64}. There are three alternative units because
i48 ≡ 3. We sometimes use the notation wi for such sets of residues that, kind of like ω-omes-for-integers, are transparent to integer i.
The modular "(i;u)-quotient"
Based on (i;u), another way to divide n by d is to euclidean-divide the integer factors
iq ≡ in .÷. id
of the quotient. Then
unit-divide to get the unit factor uq ≡ un ⋅ ud-1
of the quotient. Multiplying the two (i;u)-quotient factors yields the quotient
q ≡ iq⋅uq.
The (i;u)-quotient's divisibility condition d |iu n requires that
id .|. in AND
ud | un, which means
id euclidean-divides in with 0 remainder AND
ωud⋅ un ≡ un.
This shows that the (i;u)-quotient q ≡iu n / d
exists.
Uniqueness, just as with (c;e)-division, is achieved by re-arranging the calculation to preserve the overlap of the transparency-sets win and wid :
First calculate qo = n⋅ud-1 then complete the division as the euclidean quotient q = qo .÷. id.
(i,u) division works quite like (c,e) — sometimes with different quotients — but
the big difference
is in their definitions of divisibility: (c,e) says what I've preferred all along, that d | n
when cd .|. cn, while (i,u) on the other hand requires
id .|. in, which prevents integers from dividing units — they
can't even divide the units at the top of their own power stacks, for instance 2 (mod 72) divides every residue in C2 and in C4 with both factorizations, but 2 also (c;e)-divides the residual units
in C8 while 2 does not (i,u)-divide those units; I like that the behavior of (i;u) is totally consistent with euclidean integers — which don't divide their units ±1.
I hate that (c;e) totally ignores division by residual units — actually badly stumbles on it — but I also hate the thought of giving up the perfect (c;e) version of divisibility.
↑ to 'Deep' menu
Applications of modular division by residual integers
With (i;u)-division we can take a further look at quadratic congruences.
One algebraic approach reduces a quadratic equation into a simple square-root problem,
and adapts readily to modular:
Re-cast x2 + br + c ≡ 0 (mod m) into the form
(x + β)2 + γ = x2 + 2βx + (β2 + γ) ≡ 0.
The forms are equivalent if β ≡ b/2 and γ ≡ c − β2.
Knowing β and γ we find x from the modular square root of −γ.
There are just three issues that could get in the way of this process: First, b might not be
divisible by 2 (mod m). Second, −γ might not be a square (mod m). Third, how are square roots for residues with composite modulus?
Modular square roots are an issue on their own. Around a century ago some modular sqrt algorithms
emerged, but only for prime moduli. When m is composite, much remains to be discovered so
we need to take square roots case by case. For exploratory convenience I've been relying on an easily
written little "brute-force" complete-search applet that simply evaluates any target quadratic at every residue in the system and notes which satisfy the congruence.
The residue system Zm is much more complicated than the euclidean integer system Z and
many more surprises wait to be stumbled upon.
Applications of modular division (cont'd)
8. x2+x−12 ≡ 0 (mod 72) (Example 5 revisited)
Modular division fails at β = b/2 because in Z72 the
center c2=2 does not euclidean-integer divide the euler center c1=1.
Looking back at Example 5 we see: This same equation with same modulus was found to have four
solutions.
Residues...surprises...you know to expect.
9. Same as Example 8, but
m=63 this time.
As modulo 63 residues, 1 and 2 are both in the same cluster so each divides the other. In particular,
β ≡ 1/2 ≡ 32 (mod 63).
Next we find γ ≡ 35 (mod 63) thence x+β ≡ √28. This doesn't look
promising to a euclidean-integer-trained eye but, in fact, 28 has two square roots: 28 and 35 (mod 63).
So both x ≡ 3 and x ≡ 59 (≡ -4) are solutions.
In fact, these are the only two solutions for this modulus. How do I know that? I wrote a small
brute-force applet called "Solve Modular f(x)≡0" that searches all residues for solutions. That's how I'm doing all the modular
square roots too, since the moduli of most residue systems I care about are not prime, they're
products of powers of primes.
10. 35
x2+35
x-12 ≡ 0 (mod 63)
Search found no solutions, but the discriminant disc=b2 − 4ac ≡ 7 (mod 63) — and 7 (mod 63) truly is
square, with roots 14 and 49 (mod 63). Does x≡(-b±√disc)/(2a) ≡ (-35 ± 14)/7 ≡ 14 and 56
not yield two solutions? It does not! for instance 35⋅562+35⋅56-12≡9 not ≡0.
↑ to 'Deep' menu
IMPROVEMENTS PENDING FROM HERE ON...
↑ to 'Deep' menu
Integer division ambiguity ...
... has been resolved as of May, 2022.
Examines residues from the point of view that a residue is just an infinite set of euclidean integers.
Myself, I prefer to think of residues as a nearly independent category of numbers.
Frrraction is a product of GRS Enterprises, NLC,
a Michigan company since 1978
Most recent update of this guide: August 30, 2024, 1:30pmET
Find: From the perspective
Most recent on Frrraction: September 1, 2024, 2:15pmET
Copyright © GRS Enterprises, NLC, 2010-2023
Not void, even where prohibited. Your mileage may vary.

